Hypothesis Function and
Cost Function(가설 함수와 비용 함수)
데이터들의 집합인 가설 함수(Hypothesis Function)와 해당 데이터들의 값과
가장 오차가 적은 즉, 최소값인 θ0, θ1를 구하는 것이 비용 함수(Cost Function)이다.
비용 함수를 이용하는 이유는 수 많은 데이터들을 분류할 기준이 필요하게 되는데,
그 기준에 해당하는 선을 구해야 한다.
하지만 머신 러닝의 훈련 예제로 들어가는 데이터들이 많다.
따라서, 이 많은 데이터들을 고려했을 때의 가장 근접한 값을 구해야 한다.
이 근접한 값이 비용 함수(Cost Function) θ0, θ1이다.
따라서
가설함수의
매개변수에
해당하는
θ0, θ1를 결정해야
하는데,
비용 함수(Cost Function)의 요소 θ0, θ1 구해
hθ=θ0+θ1x 그래프를 정하면
된다.
위의 그림과 같이
θ0, θ1값에 따라
그래프가 달라지기
때문에
데이터들과 가장 근접하도록 θ0, θ1를 결정해야
한다.
따라서 위에서 여러번 언급했듯이 θ0, θ1를 결정해야 한다.
단순히 오차를 구하게 되면 음수 값이 나올 수 있기 때문에
그 값을 제곱 해 준 값을 비용 함수(Cost Function)로 한다.
비용 함수를 이용하는 이유를 다시한번 정리해보자면,
분류를 하기 위해 선을 그어야 하는데, 선을 어디다 그어야 할지 정할 수 없다.
따라서 데이터 집합들과 거리의 오차가 가장 적은 선을 구해야 하는데,
이 선의 매개변수인 θ0(y절편), θ1(x절편)를 구하기 위해 사용한다.
이렇게 구한 값들을 이용해
최종적으로 위의 그림의 가설 함수(Hypothesis Function)를 완성하면 된다.
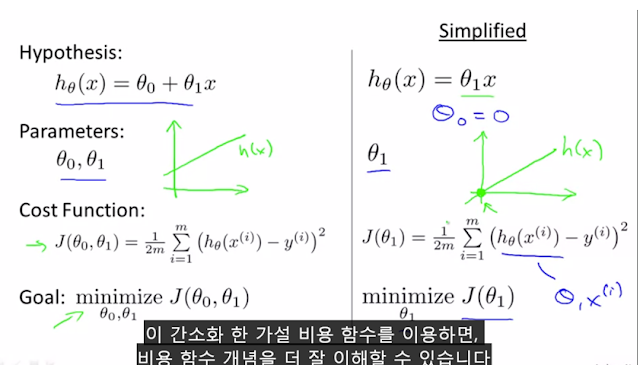
그럼 이제 예를 들어 좀 더 쉽게 이해해보자.
가설 함수(Hypothesis Function) h를 θ0=0인 경우로 단순화시킨 hθ(x)=θ1x 의
비용 함수(Cost Function) J(θ1), J(θ1) 에 대해 먼저 알아보자.
예를 들어, (1,1),(2,2),(3,3)의 데이터 집합(Training Set)을 가지고
일 때의 비용 함수를 구해본다고 가정해보자.
그렇게 된다면 각 가설 함수(Hypothesis Function)의 값은
아래의 그림과 같이 표현될 것 이다.
이 중 2번 째 가설 함수로 비용 함수를 구해본다면 아래의 그림과 같은 과정으로
비용 함수를 구할 수 있다.
동일 하게 나머지 비용 함수를 구해보면 θ0=0이고 θ1=1 일 때,
비용 함수(Cost Function)의 최소 값이 나온다.
추가적으로 많은 데이터 집합(Training Set)을
입력한다면 아래와 같은 그래프가 나온다.
위의 예보다 조금 더 복잡한 예를 살펴 보자.
이번에는 θ0,θ1이 존재하는 경우를
즉, 원래의 예시인 집의 크기와 가격이 주어진 상황이다.
θ0=50, θ1=0.06 인 경우는 가설함수 h가 아래의 왼쪽의 그림과 같이 그려지며,
J(θ0,θ1) 의 값은 왼쪽의 초록색 선들을 통해 구한 것 처럼
가설 함수와 모든 데이터 집합에 대한 길이 차이의 제곱을 합한 평균이 된다.
이러한 비용함수(Cost Function)을 일반화시켜 표현하면
θ0, θ1, J(θ0,θ1) 총 3가지를 표현해야 하므로,
아래의 그림에서 오른쪽과 같은 3차원의 그림이 된다.
그리고 이 3차원의 그림을 간단하게 바꾼다면 아래와 같은 등고선 그래프가 된다.
이 등고선 그래프는 아래와 같은 특징을 가진다.
・최소값을 갖는 θ0,θ1 는 가장 작은 타원의 중심좌표이다.
・같은 색의 곡선은 같은 J(θ0,θ1) 값을 갖는다.
즉, 가장 안쪽의 값(min)이 우리가 찾고자 하는 최적의 비용 함수 이다.
위의 등고선 그래프에서 적당히 하나 골라
가설 함수 h를 이 등고선 그래프와 비교해 최적의 비용 함수인지 확인해보자,
적당히 고른 J(θ0,θ1) 는 오른쪽 그래프의 빨간색 선과 같고,
그에 해당하는 가설 함수는 위의 왼쪽 그래프와 같다.
한눈에 봐도 많은 데이터들과 만나는 선이 아닌 것을 확인 할 수 있다.
그렇다면 이번에는 가장 최적의 비용 함수의 그래프의 경우를 보자.
위의 그림은 등고선 그래프의 가장 안쪽에 있는 최적의 J(θ0,θ1) 를 고른 것이다.
오른쪽의 그래프의 빨간선이 최적의 비용 함수 J(θ0,θ1) 이고,
왼쪽 그래프는 그의 가설 함수 h이다.
한눈에 봐도 전의 예와 비교해보자면,
많은 데이터들이 인접해 있는 것을 확인 할 수 있다.
따라서 데이터 집합(Training Set)이 주어진다면,
데이터를 분류할 선인 가설 함수 h가 필요하다.
우리는 이 가설 함수가 최적의 값이 되도록 J(θ0,θ1) 를 찾으면 된다.
