나는 손실 함수의 구현에 앞서
자료를 찾아보던 도중 손실 함수에는
교차 엔트로피라는 용어가 붙어 있는 경우가 많았다.
이에 대해 알아보려 했으나,
교차 엔트로피가 무엇 인지에 대해 찾아보기 힘들었기에
교차 엔트로피에 대한 것을 정리함과 동시에 이를 공유하려 한다.
교차 엔트로피에 대해 이야기를 나누어보기 전에
먼저 엔트로피에 대한 이해가 필요할 것이다.
그 후 교차 엔트로피에 대한 이야기를 하고,
이를 머신 러닝에서 어떻게 이용하고 있는지를 마지막으로
이번 주제에 대한 내용을 마무리 하려고 한다.
엔트로피의 기본 개념
나는 머신 러닝과 관련 없는 글을 작성할 때
엔트로피라는 말을 자주 사용 한다.
여기서 엔트로피는 해소되지 않기 때문에 쌓이고
최대로 팽창되었을 때 빅뱅과 같은 폭팔을 야기하는 어떤 음의 물체
즉, 리프킨 세계관의 엔트로피를 말한다.
이 손실 함수에서 사용하는 엔트로피는 조금 다르다.
이 엔트로피는 정보 통신 쪽의 개념으로
지금 사용되고 있는 엔트로피는 Claude Shannon에 의해 제시된 개념이다.
재미있게도 새넌의 엔트로피는 열역학의 엔트로피와 동일한 면이 있다고 한다.
열역학의 엔트로피에서 파생된 것이
리프킨의 엔트로피 세계관이기도 하기 때문에 조금은 놀라웠다.
어쨋든 정보 통신에서의 엔트로피는
전달된 메시지의 가치는 메시지의 내용이
얼마나 놀라운지에 달려 있다는 것이다.
그렇기에 어떤 사건(이벤트)이 발생할 가능성이 낮은 경우
해당 이벤트가 발생 했거나 발생할 것임을 아는 것이 더 중요하다.
발생 확률이 1에 가깝다면, 가치(놀라움)는 낮아질 것이고
발생 확률이 0에 가깝다면, 가치(놀라움)는 높아 진다.
이는 당연하다고 한다면 당연할 것이다.
왜냐하면 내가 내일 저녁밥을 먹는다는 확률은 1에 가깝다.
하지만, 내가 내일 저녁밥을 먹지 않는다는 확률은
0에 가깝기 때문에
내가 내일 저녁밥을 먹지 않는다는 정보는
주위 사람들에게는 대단히 놀라운 정보이다.
한국 내에서 북한이 미사일을 날린다는 소식은
늘 있던 일이기 때문에 가치가 낮기 때문에 엔트로피가 높을 것이며,
외국에서는 주변 국가에서 미사일을 날린다는 소식은
매우 드물기 때문에 북한이 미사일을 날린다는 소식은 매우 가치가 높은 것이다.
즉, 내가 내일 저녁밥을 먹지 않거나
외국 입장에서 북한이 미사이을 날리는 소식은 가치가 높고
그 만큼 정보 통신에서의 말하는 엔트로피는 높을 것이다.
이를 주사위 던지기와 동전 던지기의 경우를 생각해
좀 더 깊게 들어가보자.
동전은 양면 밖에 없지만,
6면이 있는 주사위는 상대적으로 더 놀랍고,
엔트로피가 크며 정보로서의 가치는 더 크다고 할 수 있다.
즉, 정보의 가치(E,엔트로피)는
확률(p)에 따라 증가하는 함수라고 볼 수 있다.
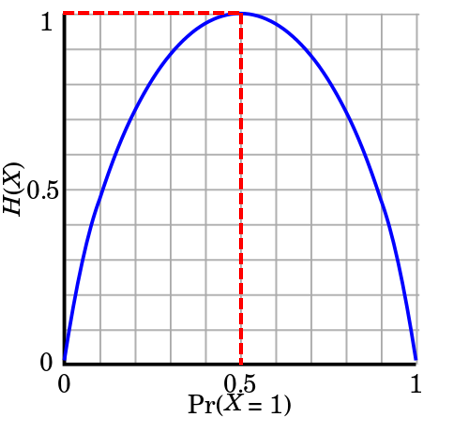
공정한 정도(Pr(X=1))에 따른
엔트로피의 값(H(X))를 나타내는 그래프 이다.
가장 공정하다고 볼 수 있는
앞면 뒷면이 존재하는 동전의 경우
최대의 엔트로피 값인 1을 얻을 수 있다.
하지만, 만약 모두 앞면의 경우
앞면이 나올 확률은 1이되며, 뒷면이 나올 확률은 0이 된다.
모두 앞면이거나 모두 뒷면인 조작된 동전의 경우,
기대할 수 있는 엔트로피의 값은 0이 된다.
왜냐하면 앞면이라고 기대했을 때
던진 동전이 모두 뒷면으로 조작되어 있다면
앞면이 나올 확률은 0이며,
반대로 뒷면이 나올 확률은 1이다.
바꿔서 뒷면이라고 기대했을 때도
던진 동전이 모두 앞면으로 조작되어 있어도 동일하다.
양면이 앞면인 동전이 앞면이 나온다고 해도,
뒷면이 나온다고 해도 전혀 놀랍지 않다.
왜냐하면 앞면이 나올 것이 뻔하기 때문이다.
좀 더 자세하게 예를 들어보자.
만약에 어떤 동전이 앞면이 나올 확률이
10%인 동전이 있다고 가정해보자.
위와 같이 0.5의 엔트로피를 얻을 수 있을 것이다.
마찬가지로 동전 앞면이 나올 확률이 90%라고 하더라도
동일하게 0.5의 엔트로피를 얻을 수 있다.
따라서 어떤 이벤트가 발생할 시에
가장 불확실할 때 혹은 각 확률이 동등 할 때
가장 큰 엔트로피를 얻을 수 있게 되며,
가장 가치 있는 정보를 얻을 수 있고
가장 놀라운 결과를 얻을 수 있다고 말할 수 있을 것이다.
정보 통신으로 말하면,
가장 큰 엔트로피를 얻을 수 있기 때문에
데이터를 보낸다고 가정했을 때,
손실 없이 데이터를 얻을 수 있다고 말 할 수 있다.
1차 세계대전 후 벨 연구소에서 일하기도 했던
전기 공학자 랠프 하틀리는
통신 엔지니어 였던 해리 나이퀴스트의 아이디어를 활용해
1928년 Transmission of Information이라는 논문에서
정보를 H로 n을 문자, 숫자 등의 수
그리고 S를 문자, 숫자 등의 선택 가능한 갯수를 s라 했을때의
엔트로피의 값을 구하는 아래와 같은 방정식을 제시 했다.
이를 동전 던지기와 주사위 던지기
그리고 문자를 보낸다고 가정했을 경우의 시점으로 살펴보자.
① 동전 던지기의 경우
좀 더 엔트로피에 대해 이해하기 위해
동전 던지기의 5번의 결과를 아래와 같이 보낸다고 가정해보자.
Alice는 클라이언트의 입장에 있고, Bob은 서버의 입장에 있다고 볼 수 있다.
여기서 밥은 예, 아니요 만으로
이 원문을 알아내야 한다고 생각해보자.
그 상황에서 첫 번째 글자가 넘어왔을 때,
밥의 경우 아래와 같은 입장일 것다.
이 상황에서 위와 같이
하나의 한 글자씩 보낸다고 가정했을때, 몇 번의 질문을 해야 할까?
밥이 선택할 수 있는 것은 앞면이냐 뒷면이냐 일 것 이다.
그렇기 때문에 이 경우 단 한번의 질문만으로 원문을 알아낼 수 있다.
왜냐하면 원문 조각이 앞면이라고 한다면,
'앞면'이라고 물어봤을 때는 엘리스가 '예'라고 대답할 것이고
원문이 앞면이라는 것을 얻어 낼 수 있을 것이고,
반대로 '뒷면'이라고 물어 봤을 때는 엘리스는 '아니요'라고 대답할 것이고
동일하게 원문이 앞면이라는 것을 확신 할 수 있기 때문이다.
그렇기 때문에 글자 수 대로 질문 한다면,
엘리스가 보내고자 하는 원문을 밥이 얻어 낼 수 있게 된다.
만약 질문의 갯수를 n,
결과값을 나타날 수 있는 경우의 수라고 가정하고,
위의 경우를 수식을 나타내면
로그 법칙에 따라
질문의 갯수가 1개라는 것을 얻어 낼 수 있다.
그리고 5번을 반복해 엘리스가 보낸 원문을 얻어낼 수 있다.
위의 기본 개념에서의 경우라면 1만큼의 엔트로피가 되며,
정보 통신에서 이 엔트로피를 1비트라고 부른다.
② 주사위의 경우
위와 동일하게 엘리스가 주사위를 5번 던진 후,
원문을 밥에게 보낸다고 가정해보자.
주사위의 경우의 수는 6개이며, 방정식에 따라 아래와 같은 수식을 도출할 수 있다.
해당 로그 값은 2.584962500721156으로 반 올림해 약 3번 질문을 한다면
원문 중 하나를 얻을 수 있을 것이다.
이로서 엘리스로 부터 5개의 주사위 값의 원문을 얻어내기 위해서는
15번의 질문이면 얻을 수 있게 된다.
③ 알파벳의 경우
사실 동전 던지기나 주사위 던지기는
실생활에서 그리 와닿지는 않는 예일 것이다.
하지만 보내야 하는 것이 영문자면 어떨까?
엘리스는 Encrypt라는 글자를 보내고 싶어 한다.
위의 그림에서 상단은 동전 던지기의 예와 동일하게
보내기 전의 엘리스의 시점을 보여주고
하단은 한 글자가 왔을 때, 밥의 시점이다.
동일하게 방정식을 사용한다면,
아래와 같이 몇 번의 질문이 필요한지를 얻어 낼 수 있다.
해당 값을 계산하면 4.700439718141093로
1번당 약 4~5번 질문을 한다면 원문에서 하나의 글자를 얻어 낼 수 있을 것이다.
이를 7번 반복해야 하니,
28~35번 질문을 한다면 7글자로 이루어진 영문자를 얻어 낼 수 있을 것이다.
하지만, 이는 엄연히 각 26개의 알파벳이 동일한 확률인
최적의 경우에 값이므로, 실제 값과는 거리가 멀 수 밖에 없을 것이다.
왜냐하면, 한글도 마찬가지겠지만
영어 또한 잘 나오는 알파벳이 있기 때문이다.
글자 뿐 만아니라 현실에서 자주 사용하는 기상 관측 정보 또한
동일한 확률로 나타나는 것이 아니기 때문에
현실에서 위의 방정식을 그대로 사용하기에는 무리가 있다.
구글의 연구 디렉터인 Peter Norvig는
Google에 보관되고 있는 도서 데이터들로 부터
단어, 단어 길이, 알파벳의 빈도를 분석했는데
가장 많은 빈도를 가진 알파벳은 E로 12.49%를 차지 했다.
[1]
조금 비약은 있을 수 있으나
단순히 이 사실만 보더라도
현실에서는 사건이 일어날 확률이 균등하지 않기 때문에
위에서 살펴봤던 방정식은 활용하기에는 다소 무리가 있으며,
더 나아가 최상의 엔트로피를 얻기란
사실상 불가능 하다는 것을 알 수 있다.
위의 그래프와 같이 1이 아닌 값들 일 것이다.
엔트로피에 대한 이해 : 클로드 섀넌
앞서 우리는 방정식에 대한 이야기를 했다.
하지만, 이는 사건이 일어날 확률이 동일 할 때에
이용할 수 있는 수식일 뿐이다.
그렇다면 어떻게 한다면
사건의 확률이 동일하지 않을 때의
엔트로피 값을 구할 수 있을까?
클로드 섀넌(Claude Shannon)은
A Mathematical Theory of Communication라는 논문에서
지금 현재 사용되고 있는 엔트로피에 대해
재정립하고 위에 대한 해답을 제시 했다.
섀넌의 이론에서는 1비트의 정보를 전송한다는 것은
받는 사람의 불확실성을 2배로 줄이는 것을 의미한다.
앞면과 뒷면이 나올 확률이 동일한 동전을 가지고
동전 던지기를 한다고 가정했을 때,
아무런 정보가 주어지지 않는다면 불확실성이 100%이지만,
누군가가 앞면이 나온다는 정보를 말했을 때
1비트의 앞면이라는 정보를 받았기 때문에,
뒷면이라는 불확실성만이 남기 때문이다.
위의 주사위 예를 잠깐 살펴보자.
위의 예에서 방정식을 이용해
모든 눈이 동일한 확률로 나올 때
한 개의 데이터 당, 약 3번 질문이면
원문을 알아낼 수 있다는 것에 대해 이야기를 나누었다.
즉, 3비트가 필요하다는 이야기가 된다.
그렇다면 주사위의 확률이 다르다면 어떻게 될까?
엘리스는 1번의 주사위를 던져, 2라는 수가 나왔고
각 주사위의 확률은 위와 같다고 가정해보자.
무엇이 올지 알 수 없는 밥의 입장은 아래와 같을 것이다.
이때 엘리스는 밥에게 3의 값이 간다고 알렸다.
그 경우 불확실성은 100%에서 10%으로 낮아져,
10배가 낮아지게 된다.
해당 로그 값은
불확실성에 의해 1비트 만큼 증가해
불확실성이 증가 했음을 알 수 있다.
이를 통해 불확실성의 값은 해당 확률의 역수이므로
즉, 1/10의 역수는 10이므로
해당 확률의 역수를 취하면 몇 배만큼 불안정성이 증가했는지 알 수 있다.
동일하게 엘리스가 밥에게 3 대신에
1이 간다고 알렸다고 가정해보자.
불확실성이 매우 감소 한 것을 볼 수 있다.
주사위의 수 만큼 위의 과정을 반복해 더 한다면
평균적으로 몇 비트의 정보를 얻어 낼 수 있는지 알 수 있는데
이를 수식화 한 것이 아래와 같다.
위의 주사위에 대한 연속된 확률 분포의 평균 비트를 구하면
2.43비트가 바로 섀넌의 엔트로피 값이다.
이 값을 모든 주사위의 수가 나올 사건의 확률이
모두 동일 했때의 값
즉, 최상의 비트인 2.5 비트를 비교 한다면 산출한 값이
얼마나 불안정한지에 대해 알 수 있을 것이다.
마치며
결론적으로 정보 통신에서의 엔트로피는
정보량이기도 하지만
컴퓨터의 근본을 이루고 있는 단위인 비트이기도 하고
위에서 방정식을 사용해 구했던 n의 갯수이기도 하다.
또한 섀넌의 방정식을 이용해 확률이 상이할 때,
평균적인 불확실성의 값을 계산해내
이를 최상의 비트와 비교 한다면,
지금 현재의 사건의 확률들이 얼마나 불확실성이 강한지에 대한
판단을 내릴 수 있을 것이다.
다음은 이번 주제의 목적이기도 한
이번에 이야기한 엔트로피를 기반으로
크로스 엔트로피에 대해 이야기를 나누어 보자.